Inertial wave modes in a cylinder
As part of my PhD I studied inertial waves in a vortex. This involved examining the modes of standing or ‘trapped’ inertial waves in a cylindrical geometry. Though this is a relatively straightforward problem, I struggled to find an expression for the frequencies and modeshapes. I ended deriving the solution myself which was a little involved, so I thought I would document it here in the hope that those who are in a similar situation in the future might find it.
This derivation appears as an appendix in my PhD thesis . I repeat it here along with some animations of the first modes and a python script for plotting the modes.
The work that it was used for appears as chapter 4 in my thesis, and is also published in APS Physical Review Fluids as Atkinson et al. (2019) with the title Dynamics of a trapped vortex in rotating convection ( PDF ). A summary of the work can be found here .
Problem setup
Here we provide the derivation for standing inertial waves in a cylindrical geometry. The solution is for a cylinder of radius \(R\) and height \(H\), axially aligned with the rotation axis. The cylinder and the fluid inside rotates at rate \(\Omega\). We seek wave solutions as perturbations to the solid body rotation. The boundary conditions on the domain are zero velocity normal to the surfaces, i.e. \(u_r = 0\) on \(r=R\) and \(u_z = 0\) on \(z = 0\) and \(z = H\).
The equations are expressed in a cylindrical coordinate system \( \left(r,\phi,z\right) \) with the velocity decomposed into poloidal and azimuthal components as follows:
\[ \boldsymbol{\mathbf{u}}_p = \left(u_r,0,u_z\right) ,,,, , ,,,, \boldsymbol{\mathbf{u}}_\phi = \left(0,u_\phi,0\right) ,, .\]
We start with the equations for angular momentum, \(\Gamma = r u_\phi\), and azimuthal vorticity, \(\omega_\phi\), in a rotating fluid neglecting viscous effects:
\[ \frac{\mathrm{D} \Gamma}{\mathrm{D} t} = -2 \Omega r u_r ,, , \]
and
\[ \frac{\mathrm{D}}{\mathrm{D} t} \left( \frac{\omega_{\phi}}{r} \right) = \frac{\mathrm{\partial} }{\mathrm{\partial} z} \left(\frac{\Gamma^2}{r^4}\right) + \frac{2 \Omega}{r} \frac{\mathrm{\partial} u_\phi}{\mathrm{\partial} z} ,, .\]
The vorticity can be written in terms of the Stokes stream function, \(\Psi\), as
\[ r \omega_\phi = - \nabla^2_* \Psi ,, ,\]
whilst the velocity can be written as
\[ \boldsymbol{\mathbf{u}}_p = \nabla \times{\left( \frac{\Psi}{r} \hat{\boldsymbol{\mathbf{e}}}_\phi \right)} = \left( -\frac{1}{r} \frac{\mathrm{\partial} \Psi}{\mathrm{\partial} z}, , , 0 , , , \frac{1}{r}\frac{\mathrm{\partial} \Psi}{\mathrm{\partial} r} \right) ,, ,\]
in cylindrical coordinates such that our boundary conditions become
\[ \left. \frac{\mathrm{\partial} \Psi}{\mathrm{\partial} z} \right|_{r=R} = 0 ,,,, , ,,,, \left. \frac{\mathrm{\partial} \Psi}{\mathrm{\partial} r} \right|_{z=0,H} = 0 ,, .\]
Further information on the poloidal-azimuthal decomposition, the Stokes operator, and a derivation of these equations from the Navier-Stokes equations can be found in chapter 2 of my PhD thesis .
Solution
We seek solutions of small amplitude which allows us to linearise the equations as follows:
\[ \frac{\mathrm{\partial} \Gamma}{\mathrm{\partial} t} = - 2 \Omega r u_r ,, ,\]
and
\[ \frac{\mathrm{\partial} }{\mathrm{\partial} t} \left( \frac{\omega_\phi}{r} \right) = \frac{2 \Omega}{r} \frac{\mathrm{\partial} u_\phi }{\mathrm{\partial} z} ,, . \]
Taking the time derivative of the vorticity equation allows it to be combined with the angular momentum equation to eliminate \(\Gamma\) and give an equation in terms of streamfunction:
\[ \frac{\mathrm{\partial}^2 }{\mathrm{\partial} t^2} \left( \nabla^2_*{\Psi} \right) = - \left(2 \Omega\right)^2 \frac{\mathrm{\partial}^2 \Psi }{\mathrm{\partial} z^2} ,, ,\]
which we can see will support waves of the form \(\Psi = \hat{\Psi}\left( r,z \right) \exp\left[ i \varpi t \right]\).
Substituting this expression results in
\[ \nabla^2_*{\hat{\Psi}} = \left(\frac{2 \Omega}{\varpi}\right)^2 \frac{\mathrm{\partial}^2 \hat{\Psi}}{\mathrm{\partial} z^2} ,, ,\]
Using separation of variables we assume that the solution can be written in the form
\[ \hat{\Psi}(r,z) = r \Psi_r (r) \sin{\left( k z\right)} ,, , \]
where \(k\) is a wavenumber \((n \pi)/H\).
Substituting this results, after some algebra, in
\[ r^2 \frac{\mathrm{\partial}^2 \hat{\Psi}_r}{\mathrm{\partial} r^2} + r \frac{\mathrm{\partial} \Psi_r}{\mathrm{\partial} r} + \left( \eta^2 r^2 - 1 \right) \Psi_r = 0 ,, , \]
where
\[ \eta = k \sqrt{\left( \frac{2\Omega}{\varpi} \right)^2 - 1} ,, , \]
which we recognise as a Bessel equation with the solution
\[ \Psi_r = C_1 J_1\left( \eta r \right) + C_2 Y_1\left( \eta r \right) ,, .\]
We require solutions to remain finite at the axis which tells us that \(C_2 = 0\). Applying the radial boundary condition results in
\[ \eta R = \zeta_m ,, ,\]
where \(\zeta_m\) is the mth zero of the Bessel function \(J_1\). Rearranging this tells us that the frequency of the oscillations for the mode \(\left( r,z \right) = \left( m,n \right)\) is
\[ \varpi_{m,n} = \frac{2 \Omega}{\sqrt{1 + \left(\frac{H\zeta_m}{n \pi R}\right)^2}} ,, ,\]
which is consistent with the requirement that inertial waves have a frequency between \(0\) and \(2,\Omega\).
Finally this allows us to write down an expression for the streamfunction of the mode \(\left( m,n \right)\) as being
\[ \Psi_{m,n} = A , r , J_1\left( \frac{\zeta_m}{R} r \right) \sin{\left( \frac{n \pi}{H} z \right)} , e^{\left( i \varpi_{m,n} t \right)},, ,\]
from which we can obtain expressions for \(\Gamma\), \(\omega_\phi\), and \(\boldsymbol{\mathbf{u}}_p\).
Plotting of modes
I wrote a short python script to calculate and plot the various modes for visualisation. Shown below are animations of the first four modes from \((1,1)\) to \((2,2)\) in a sphere of \(R = H = 1\). The contours on the left hand side show the poloidal streamfunction, whilst those on the right show angular momentum. The colour on the right indicates the azimuthal vorticity. The intervals and limits are the same in all cases.
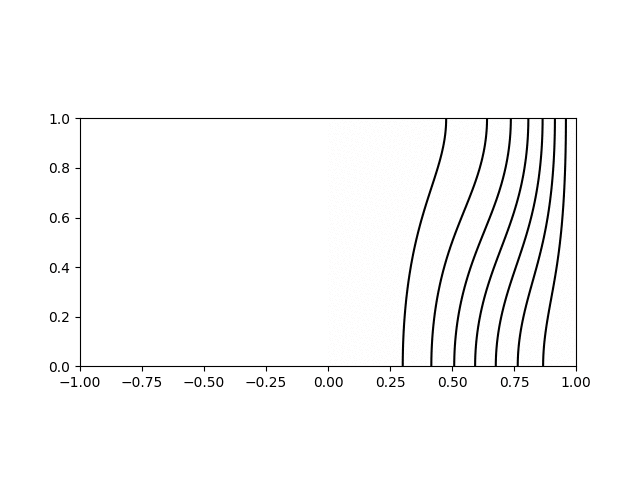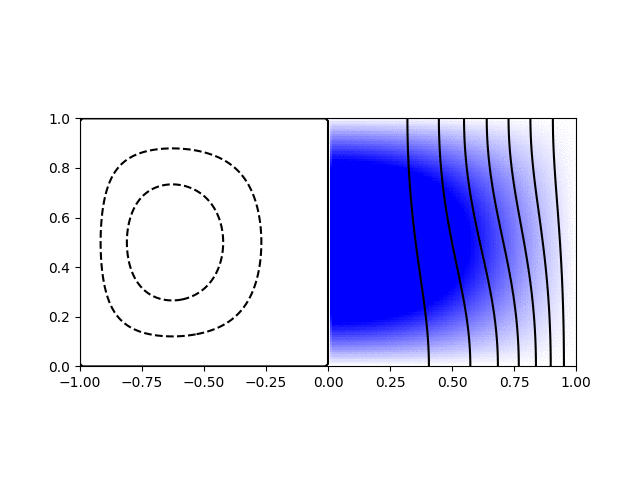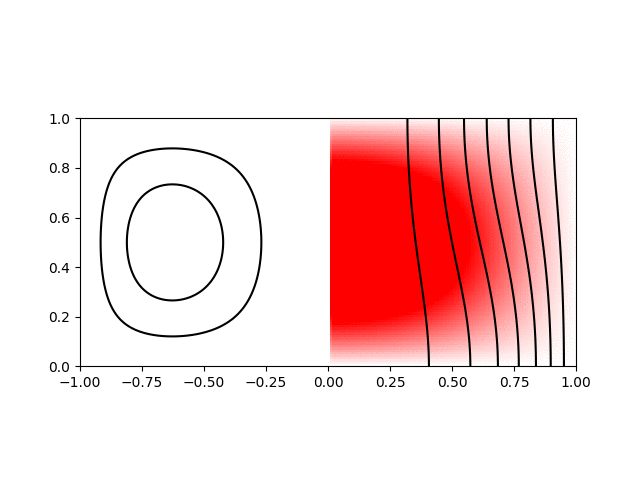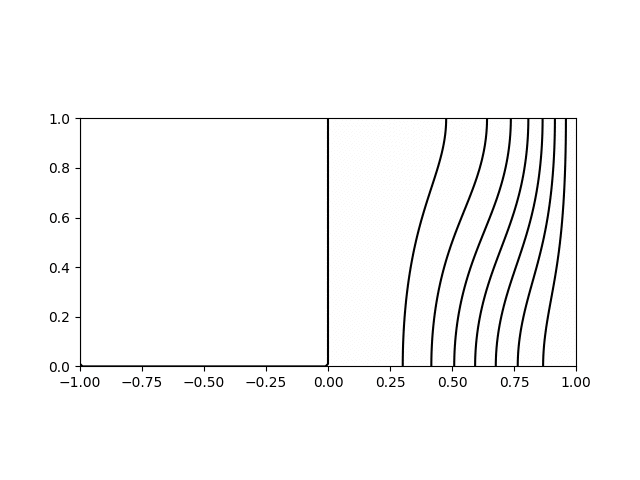
Inertial wave mode \((r,z) = (1,1)\) with \(\varpi/\Omega=1.27\)
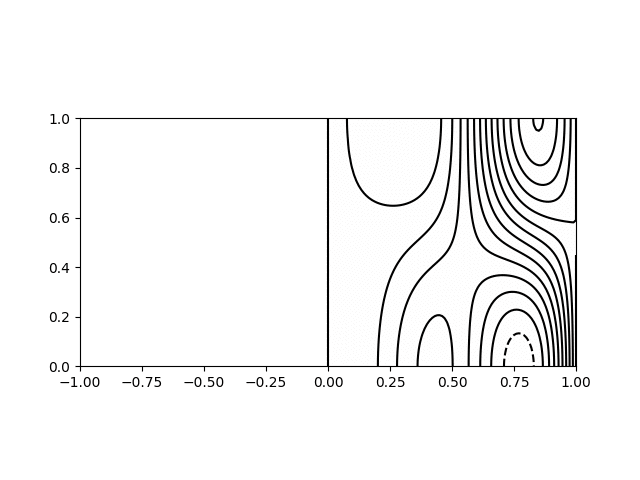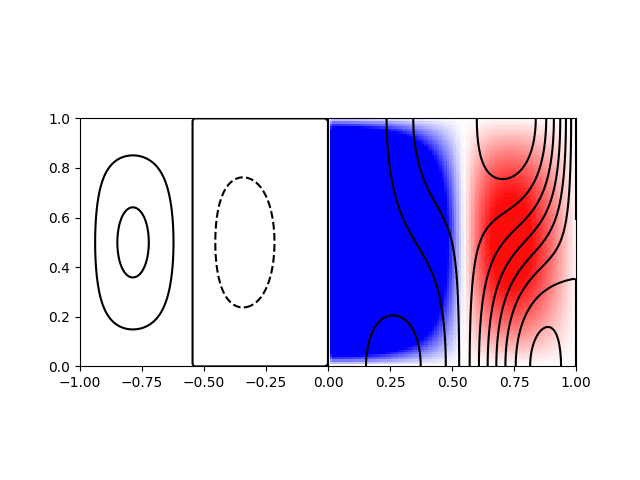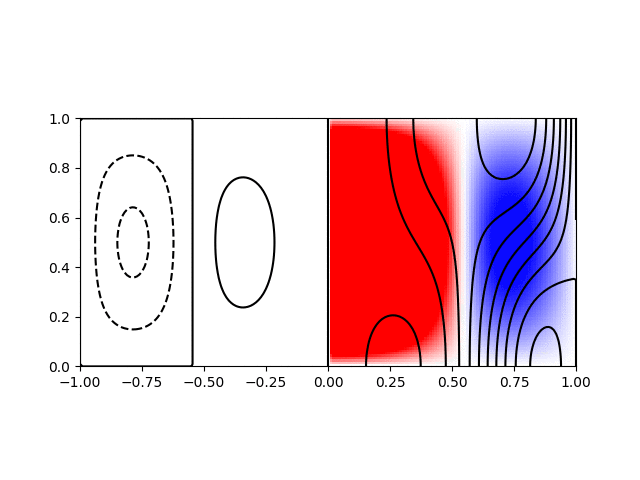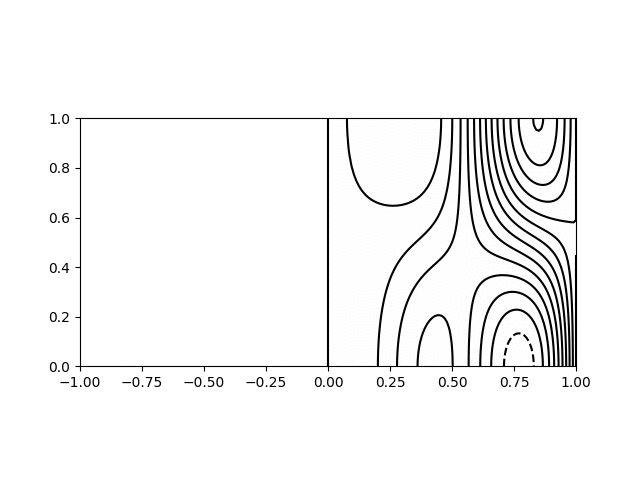
Inertial wave mode \((r,z) = (2,1)\) with \(\varpi/\Omega=1.71\)
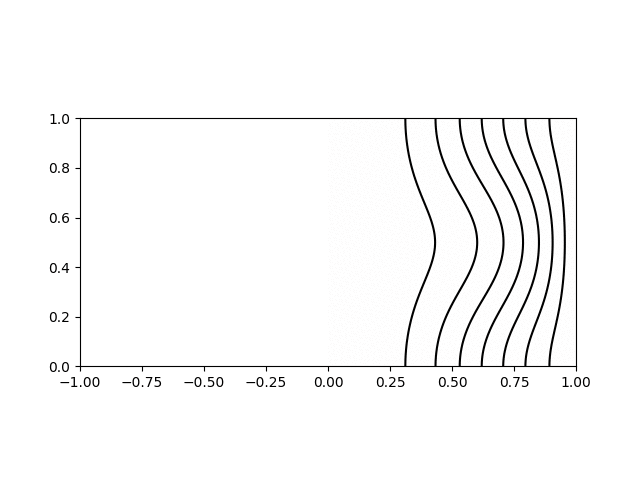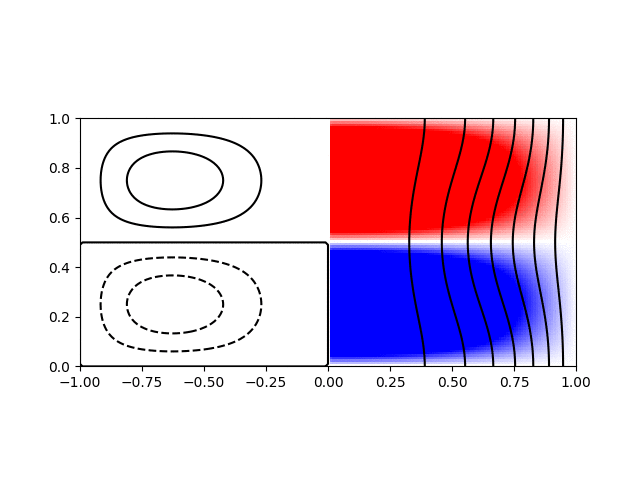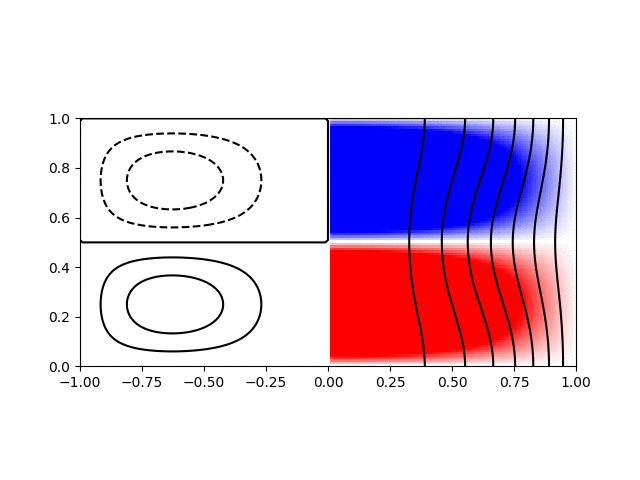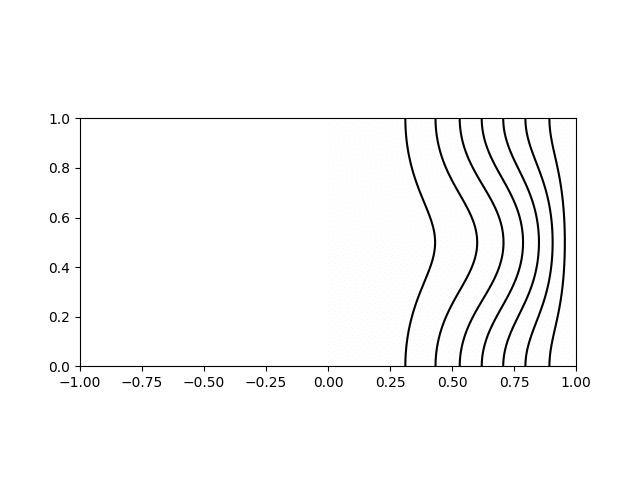
Inertial wave mode \((r,z) = (1,2)\) with \(\varpi/\Omega=0.82\)
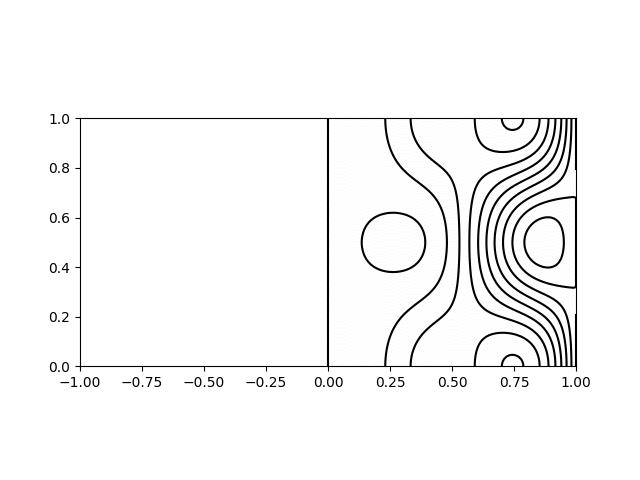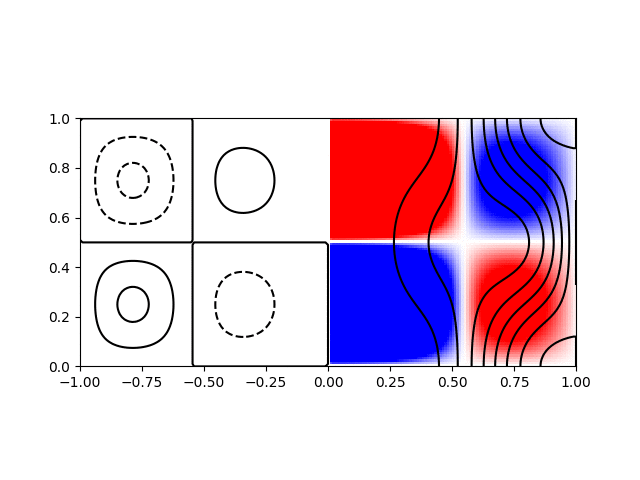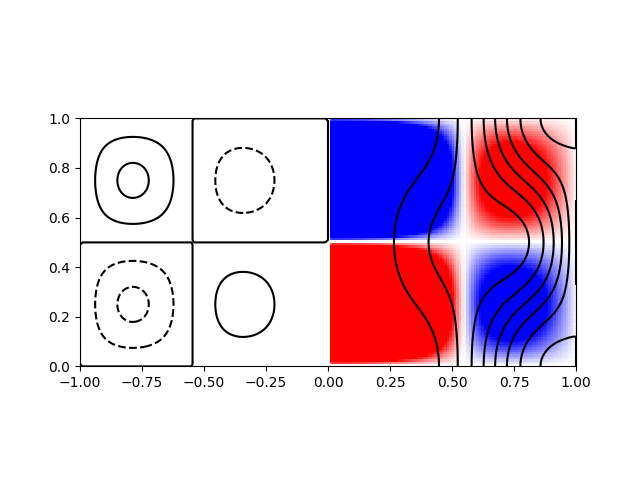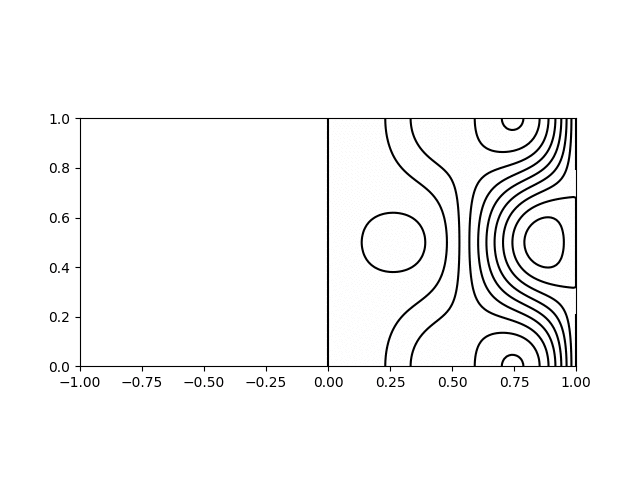
Inertial wave mode \((r,z) = (2,2)\) with \(\varpi/\Omega=1.33\)